SPSS Bağımsız T Testi

By istatistikavm.com
In İstatistik Analiz
0
Share

Bağımsız T Testi veya bağımsız ya da eşleştirilmemiş, örneklem t-testi birbirinden bağımsız iki nümerik veri setinin ortalamalarının birbirine eşit olup olmadığını belirlemek için kullanılan istatistiksel bir hipotez testidir. Bu hipotez testinde esas (H0) ve alternatif (H1) hipotez aşağıdaki şekilde kurulur:

Bağımsız T Testi Hipotezleri

H0: µ1 = µ2

H1: µ1 ≠ µ2 veya µ1 > µ2 veya µ1 < µ2

µ1 ve µ2 , 1. ve 2. veri setinin ortalamalarını göstermektedir. Elde edilen test istatistiği, t dağılımına göre bakılarak elde edilen t’nin kritik t değerleri bölgesinin içinde olup olmadığına bakılır. Elde edilen t, kritik t bölgesinin içindeyse, esas hipotez belirlenen güven aralığında reddedilir. Aksi halde esas hipotezi reddedecek bir kanıt bulunamadığı sonucuna bakılır. Testin özgürlük derecesi, (toplam numune boyutu)-1 olur. Test istatistiği, ‘(toplam numune boyutu)-1’ özgürlük derecesine karşı gelen t-dağılımındaki kritik bölge ile karşılaştırılır. Bağımsız t-testi istatistiği eşit boyutlu veya farklı boyutlu veri setleri için farklı şekillerde elde edilmektedir:

Eşit boyutlu veri setleri için, t= (X1– X2)/(Sp/(2/n)0.5), Özgürlük derecesi = 2(n-1)

Farklı boyutlu veri setleri için, t= (X1– X2)/(Sp/((1/n1)+ (1/n2))0.5), Özgürlük derecesi = n1 + n2 – 2

X1 ve X2, veri setlerinin ortalamasını, Sp veri set havuzunun standart sapmasını, n eşit boyutlu veri setlerinden birinin boyutunu, n1 ve n2 birinci ve ikinci veri setinin boyutunu göstermektedir. Denklemden elde edilen test istatistiği, ilgili özgürlük derecesine karşı gelen t-dağılımındaki kritik bölge ile karşılaştırılır.

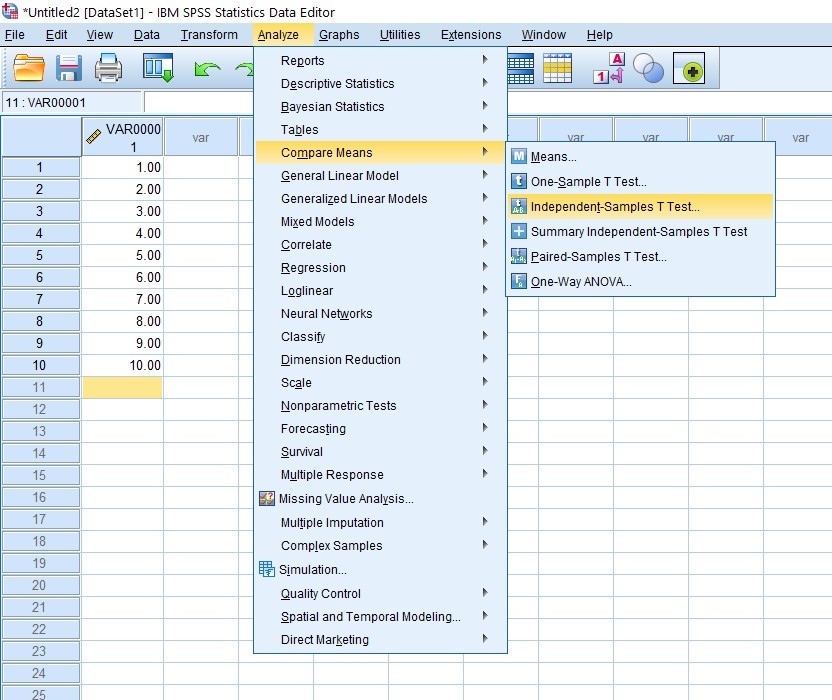
SPSS’de ilgili komutları kullanarak (Şekil 1) bağımsız t-testi yapabilmek mümkündür.

Bağımsız T Testi
Figure 1. SPSS’de bağımsız t-testi sekmesi

 

“…F-testi, esas hipotezin test istatistiğinin F-dağılımına bağlı olduğu bütün testleri içerir. Genellikle aşağıdaki alanlarda kullanılır:

F-Testi Kullanım Alanları
1. Normal dağılım gösterdiği kabul edilen, n ve m boyutlu iki veri setinin varyansları oranının bire eşit olup olmadığının sınanması.

Bu şekilde elde edilen varyans oranının F test istatistiği olmakta ve dolayısıyla F dağılımına bağlı olmaktadır. Esas hipotez, F değerinin bire eşit olup olmadığı üzerine kurulur. Eğer test istatistiği, (n-1) ve (m-1) özgürlük derecelerine denk gelen F dağılımında kritik F bölgesinin içine giriyor ise esas hipotez reddedilir, yani iki varyansın birbirine eşit olduğu reddedilir. Aksi takdirde iki varyansın birbirinden farklı olduğuna dair bir kanıt bulunamadığı sonucuna varılır…”

F Testi ile ilgili yazının devamı için lütfen tıklayınız!

Related Posts
spss analiz istanbul

SPSS Analiz İstanbul

By istatistikavm.com
In İstatistik Analiz
0

SPSS Analiz İstanbul ile etkili ve verimli SPSS yardımı alabilirsiniz. SPSS Analizi (Statistical Package for the Social Sciences), IBM şirketine ait olan ve istatistiksel analiz için kullanılan bir programdır. Genellikle sosyal bilimler alanında çeşitli uygulamalarda, örneğin pazar ve anket araştırmaları, kullanılsa da tıp, eğitim ve mühendislik alanlarında da sıklıkla kullanılan bir programdır. Ayrıca, SPSS, yüksek lisans ve doktora öğrencilerinin tez çalışmalarında, tezlerindeki verilerin analizi için sıkça kullandıkları bir uygulamadır. SPSS programında aşağıdaki istatistiksel analizler (Şekil 1) rahatlıkla yapılabilmektedir:

a) Raporlar

b) Tanımlayıcı istatistikler: Cross tabulation (çapraz tabulasyon); frequencies (frekanslar); descriptives (tanımlayıcılar), P-P ya da Q-Q grafikleri, v.s.

c) Bayesian İstatistikleri: Tek yön-Anova testi, Pearson korelasyonu, Tek Örnek Normal ya da Binomial Analizi, v.s.

d) Tablolar: Çoklu cevap setleri

e) Ortalama karşılaştırma: eşleştirilmiş t-testi, tek örnekli t-testi, bağımsız örnekli t-testi, v.s.

f) Genel lineer modelleme ya da genelleştirilmiş lineer modelleme: Tek değişkenli, çok değişkenli, v.s.

g) Karışık modeller: Lineer, genelleştirilmiş lineer modeller

h) Korelasyon: İki degiskenli, kısımsal, uzaklıklar, kanonik uzaklıklar…

ı) Regresyon analizleri: Lineer regresyon, non-lineer regresyon, v.s.

i) Parametrik olmayan testler

j) Diğer analizler (Mekansal ve zamansal modelleme, kalite kontrol analizi, güvenilirlik analizi, sınıflandırma, tahmin, kurtulma analizleri, boyut küçültme, çoklu cevap ve tahmin analizleri v.s.

Ayrıca verininin veya veriden elde edilen istatistiksel sonuçların grafiksel çıktılarını, SPSS’deki chart builder, sekmesi (Şekil 2) kullanılarak oluşturulabilir. Elde edilen bu grafikler, veriyi niteliksel veya niceliksel olarak keşfetmek amacıyla kullanılabilir.

spss analizi
Şekil 1. SPSS’de yapılabilen istatistiksel analizler

 

spss analizi
Şekil 2. SPSS içersinde grafik oluşturmanızı sağlayan chart builder sekmesi

 

SPSS’de veri analizi, grafiksel bir kullanıcı arayüzü (Şekil 3) üzerinden açılır menüler yardımıyla kolaylıkla yapabilir. Ayrıca SYNTAX adlı kendi proglama arayüzü (Şekil 4) veya kendinde gömülü PYTHON derleyici (Şekil 5) yardımıyla kullanıcılar kendi amaçları doğrultusunda programda makro uygulamalar çalıştırabilir. Böylece, SPSS’de veri analizi çok daha geniş bir kapsamda yapılabilir. SPSS; Windows, Mac OS X ve Linux işletim sistemlerinde çalıştırılabilir. Ancak, programın genelde Windows sürümü diğerlerine göre daha kullanışlıdır.

SPSS Analiz İstanbul, SPSS programıyla başarılı bir analiz yapmak için kullanıcıların (a) Python dili programlaması hakkında bilgi sahibi olması, (b) SPSS’e veri girişi ve biçimlendirmesi (Şekil 6) yapabilmesi, (c) veriye uygulanacak doğru analizin seçilmesi ve verinin bu analize uygunluğunun belirlenmesi, (d) analizin veriye doğru olarak uygulanması ve (e) kullanıcının istediği analiz çıktılarının alınması gerekmektedir. SPSS, üstte de bahsedildiği gibi birçok karmaşık istatistiksel analizi uygulayabilen sofistike bir program olduğu için SPSS analizlerinin bu yazılımda uzman kişiler tarafından yapılması verinin daha başarılı analiz edilmesine yol açacaktır.

 

spss analizi
Şekil 3. SPSS genel arayüzü

 

spss analizi
Şekil 4. Syntax Arayüzü

 

spss analiz istanbul
Şekil 5. SPSS Python Programlama Kabuğu

 

spss analiz istanbul
Şekil 6. SPSS Veri Biçimlendirme Sayfası

 

bağımlı t testi

SPSS Bağımlı T Testi

By istatistikavm.com
In İstatistik Analiz
0

Bağımlı ya da eşleştirilmiş, örneklem t-testi birbiriyle eşleşen, dolayısıyla birbirine bağımlı, iki nümerik veri setinin ortalama farkının sıfır olup olmadığını, yani veri setlerinin ortalamalarının birbirine eşit olup olmadığını belirlemek için kullanılan istatistiksel bir hipotez testidir. Eşleştirilmiş t-testlerinde, ya boyutları eşit iki veri setinin ortalaması, ya da bir veri seti ölçülmüş tekrarı karşılaştırılabilir. Bu hipotez testinde esas (H0) ve alternatif (H1) hipotez aşağıdaki şekilde kurulur:

Bağımlı T Testi Hipotezleri

H0: µ1 – µ2 = 0

H1: µ1 – µ2 ≠ 0 veya µ1 – µ2 > 0  veya µ1 – µ2 < 0

µ1 ve µ2 , 1. ve 2. veri setinin ortalamalarını göstermektedir. Elde edilen test istatistiği, t dağılımına göre bakılarak elde edilen t’nin kritik t değerleri bölgesinin içinde olup olmadığına bakılır. Elde edilen t, kritik t bölgesinin içindeyse, esas hipotez belirlenen güven aralığında reddedilir. Aksi halde esas hipotezi reddedecek bir kanıt bulunamadığı sonucuna bakılır. Testin özgürlük derecesi, iki veri seti birbirine bağımlı olduğu için (numune boyutu/2)-1 olur. Test istatistiği, (numune boyutu/2)-1 özgürlük derecesine karşı gelen t-dağılımındaki kritik bölge ile karşılaştırılır. Elde edilen test istatistiğinin formülü aşağıdaki şekildedir:

t= (Xf – (µo = 0))/(SD/n0.5)

Xf, eşleşmiş veri farklarının ortalamasını, SD eşleşmiş veri farklarının standart sapmasını ve n eşleşmiş veri çiftlerinin sayısını göstermektedir. Denklemden elde edilen test istatistiği, n-1 özgürlük derecesine karşı gelen t-dağılımındaki kritik bölge ile karşılaştırılır. SPSS’de ilgili komutları kullanarak (Şekil 1) bağımlı t-testi yapabilmek mümkündür.

bağımlı t testi
Figure 1. SPSS’de bağımlı t-testi sekmesi

 

“…Bağımsız T Testi veya bağımsız ya da eşleştirilmemiş, örneklem t-testi birbirinden bağımsız iki nümerik veri setinin ortalamalarının birbirine eşit olup olmadığını belirlemek için kullanılan istatistiksel bir hipotez testidir. Bu hipotez testinde esas (H0) ve alternatif (H1) hipotez aşağıdaki şekilde kurulur:

Bağımsız T Testi Hipotezleri

H0: µ1 = µ2

H1: µ1 ≠ µ2 veya µ1 > µ2 veya µ1 < µ2

µ1 ve µ2 , 1. ve 2. veri setinin ortalamalarını göstermektedir. Elde edilen test istatistiği, t dağılımına göre bakılarak elde edilen t’nin kritik t değerleri bölgesinin içinde olup olmadığına bakılır. Elde edilen t, kritik t bölgesinin içindeyse, esas hipotez belirlenen güven aralığında reddedilir. Aksi halde esas hipotezi reddedecek bir kanıt bulunamadığı sonucuna bakılır…”

Bağımsız T Testi yazısının devamı için lütfen tıklayınız!

Bir cevap yazın

E-posta hesabınız yayımlanmayacak.

Call Now Button