İstatistiksel analiz sistemli bir şekilde sayısal veriler toplamaktır. Belirli bir amaç için çeşitli veriler toplanır. Bu veriler tablo ve grafik haline getirilir. Sonuçlar sınıflandırılır ve çözümlenir. Son olarak ortaya çıkan bu sonuçlar yorumlanarak veriler arası ilişkilere ve genellemelere ulaşılır. Elde edilen sonuçlar gözlem yapmaya ve geleceğe yönelik varsayımlarda bulunmaya yardımcı olur.
İstatistik, iş dünyasından ekonomi platformuna, kamu araştırmalarından vergi sistemlerine kadar pek çok alanda uygulanabilir bir bilim dalıdır. İstatistiğin temel amacı, detaylı araştırmalar sonucu elde edilen verilerin istatistiksel analiz yöntemleriyle en doğru şekilde ve amaca uygun olarak yorumlanabilmesidir.

İstatistiksel çalışmaların ortak noktalarından biri nedenselliği bulmak ve bağımsız değişkenlerdeki bir değişimin bağımlı değişken üzerindeki etkilerini incelemektir. Nedenselliği ele alan temelde iki tür ana istatistiksel yöntem bulunur. Bunlar deneysel çalışmalar ve gözleme dayalı çalışmalardır.
İki çalışma türünde de bağımsız değişken veya değişkenlerdeki farklılıkların, gözlenen bağımlı değişken üzerindeki etkisi incelenir. Bu çalışma türlerinde oluşan fark ise yöntemin uygulanma biçimidir. Yöntemlerin ikisi de sağlıklı veriler ortaya koyabilir.
Deneysel çalışmalar sırasında araştırmaya konu sisteme dışarıdan müdahele edilebilir. Sistemde yapılacak bilinçli değişikliklerle bağımsız değişkenlerden kaynaklanan farklılıkların, bağımlı değişken üzerindeki etkiler incelenebilir. Gözleme dayalı çalışmalarda durum tam tersidir. Araştırma konusu sisteme kesinlikle müdahale edilmez. İstatistiksel yöntemler kullanılarak veriler toplanır. Bağımlı ve bağımsız değişkenler arasındaki ilişkiler çözümlenir.
İstatistiksel analiz yöntemleri, toplanan verilerin anlamlandırılmasına ve açıklanmasına yardımcı olur. Bunun için genel olarak 5 temel istatistiksel analiz yöntemi kullanılır.
İSTATİSTİKSEL ANALİZ YÖNTEMLERİ
1- BETİMSEL ANALİZ YÖNTEMİ
Betimsel analiz yöntemi araştırmaların ilk basamağıdır. İlgili veriler toplanır ve çözümlenir. Araştırmalar sonucunda ulaşılan sayısal veriler grafik veya tablo halinde özetlenir. Betimsel analizin temel hedefi ulaşılan veri değerlerini veya sıralaması yapılmış bir veri setini tablo, grafik veya nicel şekilde ifade etmektir. Bu yöntem çeşitli tablolardan ve grafiksel araçlardan faydalanır. Ortalama, Aritmetik Ortalama, Mod, Medyan, Standart Sapma, Varyans ve Korelasyon Katsayısı betimsel analizde kullanılan temel ölçülerdir.
|
Betimsel Analiz Araçları |
|
|
Tablolar |
Grafiksel Araçlar |
| Sıklık Sayımı Tablosu | Çubuk Grafik |
| Sıklık Dağılımı Tablosu | Kutu Grafik |
| Çok Sayılı Özetleme Tabloları | Saçılım Grafiği |
| İki-Yönlü Sınıflandırma Tablosu | Sütun Grafik |
| Çoklu-Yönlü Sınıflandırma Tabloları | Q—Q Tablosu |
2- ÇIKARIMSAL ANALİZ YÖNTEMİ
Çıkarımsal analiz yönteminde elde edilen veriler ve ortaya çıkan sonuçlar üzerinde çıkarımlar yapılır. Araştırmalar sonucu elde edilen veriler ve bu verilerin dağılımının özellikleri anlama sürecine dahil edilir, tümevarım mantığıyla anakütle hakkında çıkarımlara ve varsayımlara ulaşılır. Elde edilen veriler hedef anakütleyi ifade eden örneklem olarak kabul edilir. Bu yöntem çıkarımsal kestirim ve parametrik/parametrik olmayan hipotez testlerinden faydalanır.
Çıkarımsal Kestirim; momentler yöntemi, en büyük olabilirlik, en büyük artçıl, Bayes-tipi kestirimci , minimum uzaklık, maksimum aralık verme, kestirim, güven aralığı ve inanılır aralık kavramlarını kapsar.
3- FARK ANALİZİ YÖNTEMİ
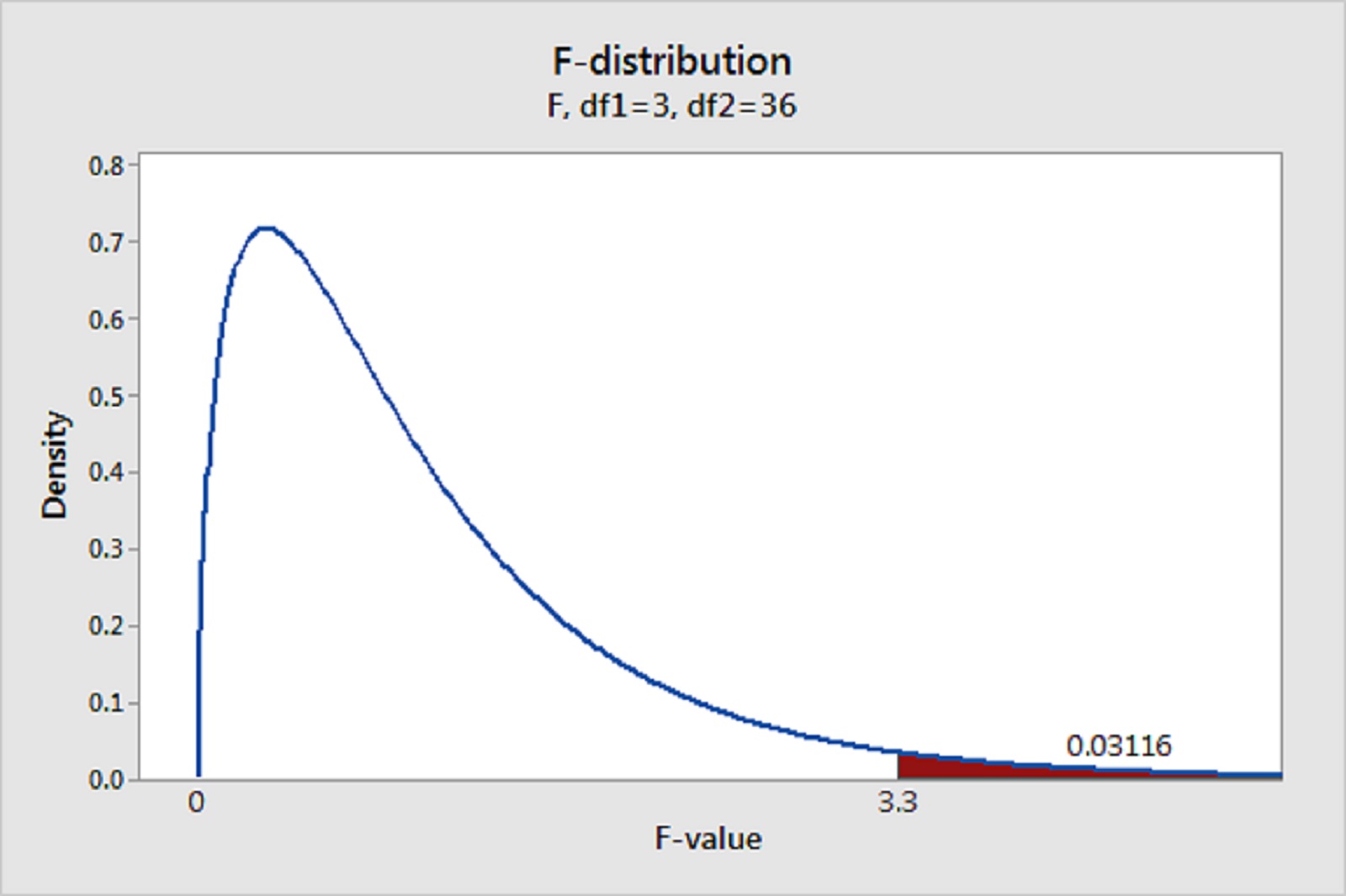
Araştırmaya konu olan iki grup arasında farklılık olup olmadığı, eğer farklılık varsa bunun hangi sebeplerden kaynaklandığı hakkında istatistiksel verilere ulaşmayı sağlayan analiz yöntemidir. Grup ortalamaları, gruplar içi/gruplar arası varyasyonlar ve bunlara bağlı olan işlemleri analiz etmek için kullanılır. Araştırma konusu gruplar arasındaki farklılıkların tespitinde F Testi, T Testi ve Varyans Analizi kullanılır. Varyans Analizi, ANOVA olarak da isimlendirilir. ANOVA, anakütle ortalamaları arasında farkın olup olmadığını denemek için kullanılır.
Varyans analizi deneysel verilerin analiz edilmesi için özellikle pratikte çok defa tercih edilen özel bir istatistikel hipotez denemesi şeklidir. Varyans Analizi’nde verinin normal dağılım gösteren bir anakütleden geldiğini ve ancak farklı ortalamalar dolayısıyla ayrım yapılabileceğini varsayan Sabit Etki Modeli; verinin bir farklar hiyerarşisi ile sınırlanmış olan değişik hiyerarşi içeren anakütlelerden geldiğini varsayan Rastgele Etki Modeli; sabit etkileri hem de rastgele etkiler kapsayan Karışık Etki Modeli kullanılır.
4- İLİŞKİ ANALİZİ YÖNTEMİ
Üzerinde araştırma yapılan veriler arasındaki ilişkileri tespit etmekte kullanılan bu yöntem, değişkenler arasındaki sistematik bağlantıların çözümlenmesinde yardımcı olur. Çapraz tablolama ve korelasyon tekniklerini içerir.
Korelasyon, olasılık kuramı ve istatistikte iki rastgele değişken arasındaki doğrusal ilişkinin yönünü ve gücünü belirtir. Genel istatistiksel kullanımda korelasyon, bağımsızlık durumundan ne kadar uzaklaşıldığını gösterir. Farklı durumlar için farklı korelasyon katsayıları geliştirilmiştir. Bunlar arasında en popülerleri Pearson çarpım-moment korelasyon katsayısı ve Sıralama korelasyonu katsayıdır.
Pearson çarpım-moment korelasyon katsayısı iki değişkenin kovaryansının, yine bu değişkenlerin standart sapmalarının çarpımına bölünmesiyle elde edilir. Korelasyon katsayısı, bağımsız değişkenler arasındaki ilişkinin yönü ve büyüklüğünü belirten katsayıdır.
Bu katsayı, (-1) ile (+1) arasında bir değer alır. Pozitif değerler direkt yönlü doğrusal ilişkiyi; negatif değerler ise ters yönlü bir doğrusal ilişkiyi belirtir. Korelasyon katsayısı 0 ise söz konusu değişkenler arasında doğrusal bir ilişki bulunmaz.
Pearson’un korelasyon katsayısı iki değişken arasındaki doğrusal ilişkinin gücünü göstermekle beraber, kestirim olarak bulunan katsayı değeri bu ilişkiyi tam olarak açıklamak için yeterli değildir. Bu sonuç eğer veriler normal dağılım göstermiyorlarsa daha da önem kazanmaktadır.
Sıralama korelasyonu ise istatistik bilimi içinde aynı istatistik birimlerinin değişik kriter değişkene göre iki değişik sıralama arasında bulunan bağlantıyı inceler. Örneklem verisi kullanarak hesaplanan sıralama korelasyon katsayısı iki sıralama arasındaki doğrusal ilişkiyi ölçer ve elde edilen katsayının istatistiksel anlamlılığını değerlendirir.
En çok kullanılan iki sıralama korelasyon katsayısı, Spearman’in ρ (rho) Sıralama korelasyon katsayısı ve Kendall’in τ (tau) sıralama korelasyon katsayısıdır. Her iki katsayı da [-1, +1] aralığı içinde tek bir değer alır. Katsayı değeri -1 ise birinci sıralama ikinci sıralamanın tümüyle tersidir ve iki seri sıralaması arasında mükemmel anlaşmazlık bulunur. Katsayı değeri 0 ise iki sıralama birbirinden tümüyle bağımsızdır. Son olarak eğer katsayı değeri +1 ise birinci sıralama ikinci sıralamanın tümüyle aynıdır ve iki seri sıralaması birbiriyle aynıdır. Sıralama korelasyon katsayısı ne kadar büyük olursa sıralamalar arasındaki uyum o denli büyük olur.
5- TAHMİN ANALİZİ YÖNTEMİ
İstatistiksel araştırmalar sonucu elde edilen verilerin kullanılarak geleceğe yönelik tahminlerde bulunulmasına olanak sağlar. Regresyon analizi tekniklerinden faydalanılır. Regresyon analizi, iki ya da daha çok değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Değişken sayısına göre tek değişkenli regresyon veya çok değişkenli regresyon olarak adlandırılır.
Regresyonda, değişkenlerden biri bağımlı diğerleri bağımsız değişken olmalıdır. Regresyon; Doğrusal ve Doğrusal Olmayan olarak ikiye ayrılır.
Doğrusal regresyon; anakütle doğrusal regresyon modeli, İki değişkenli regresyon katsayı kestirimleri, çok değişkenli regresyon katsayı kestirimleri, hatalar varyansı ve toplam kareler, kestirim denklemin genel uyum iyiliğinin çıkarımsal kontrolü, interpolasyon ve ekstrapolasyon, ağırlıklı en küçük kareler yöntemi, değişkenlerde-hatalar modeli, genelleştirilmiş doğrusal model, güçlü regresyon ve ayrık bağımlı değişken gibi işlemler ve bunların alt dallarını barındırır.
Testleri; sıfır hipotez, I. tür ve II. tür hata, anlamlılık seviyesi ve p-değeri gibi kavramlar içerir. Hipotez testlerinde değişkenin tek veya ikili oluşuna ve parametrik olup olmamasına göre μ testi, π testi, μ1-μ2 testi, π1-π2 testi, medyan testi, ki-kare testi, Pearson ki-kare testi, Phi katsayısı, σ1/σ2 testi, Wald testi, Mann-Whitney U testi ve Wilcoxon’in işaretli sıralama testi gibi testler uygulanır.